Any study has to be concerned with the signal-to-noise ratio, even if we often don’t explicitly measure it. For any phenomenon we want to measure, we accordingly must ask of our measurements: how much of what I’m seeing is driven by randomness? How much is real, non-random signal that reflects the thing I’m trying to measure?
eDNA amplicons are a fairly noisy kind of data. We know this because we sequence individual PCR replicates; the same environmental sample, amplified and sequenced in triplicate, yields somewhat different reflections of the biological community under study. Because these observations arise from literally the same environmental sample, we know the variation among them is noise, rather than signal. This noise is the observation variance due to the combination of PCR and sequencing. If there were no such variance, our replicates would all look identical. [Note: because thinking about multivariate data can make your brain hurt, here we’re treating observations of each taxon as if they are independent of the others, but that’s not really true… the data are compositional, because of finite read-depth. More on this in the future.]
We can express this variance in terms of the difference in communities –- e.g. Bray-Curtis or other ecological (dis)similarity metrics –- or by changes in the number of species detected, etc., or else by looking at the variation in the abundance of individual sequence variants.
In terms of the difference between observations of whole communities (all observed taxa; Bray-Curtis or other), we consistently see dissimilarities of 0.25-0.4 among technical replicates in our datasets. So, on average, we would need to see changes in Bray-Curtis values larger than this between different environmental samples in order to confidently detect any true signal of community change.
At the level of individual sequence-variants (ASVs; or OTUs, or taxa, or whatever your individual unit of study), we can dig into the analysis a bit more deeply. If we treat sequence reads as being distributed according to a negative binomial distribution for a given ASV i, the probability of seeing a given number of reads nReads_i is
nReads_i∼NegativeBinomial(μ_i,ϕ)
And we know replicates from the same sample have a common μ_i, because they are repeated estimates of that same shared phenomenon in the world. The variability in our observations of the world due to the vagaries of PCR and sequencing, then, is captured by ϕ.
If we know ϕ, we can rationally distinguish signal from noise at the level of individual ASVs, estimating which ASVs contain enough signal that we can confidently use them to measure change in the world, and conversely, which ASVs are unreliable indicators of that change (i.e., noise). (Richness is a separate question… ϕ may change the likelihood of detecting a given ASV/taxon, but it does not speak to the likelihood of an observed ASV being a true or false detection). Moreover, if we know ϕ, there’s an argument to be made that we don’t have to sequence individual replicate reactions, saving time and money and sanity.
An Example
Suppose we observe sequence reads from a beaver (Castor canadensis) in a set of three replicate reactions stemming from a common environmental sample in Creek A. Our read-counts in these triplicates are 132, 47, and 90, respectively. At Creek B, we observe beaver read-counts of 52, 73, and 14. (Assume, for simplicity, that read-depth across all replicates is identical; in reality we can account for variable read-depth using another parameter in the model). Fitting probability distributions to these observations lets us ask questions such as: are we confident that Creek A has a greater signal of beaver than Creek B does, given the observation variation?
To start, let’s fit those distributions and plot the results:

These curves capture the variability in our observations at each creek, and they suggest that Creek A indeed has an expected value greater than Creek B (fitted ML values of μ: 89.67 vs. 46.33). But this doesn’t take into account the variability around those means… that is, our noise (ϕ ; fitted values of ϕ are 6.51 and 2.75, respectively).
We can sample from the fitted probability distributions to get a quick estimate of the difference between them:

And the estimated probability that Creek A has a truly greater number of beaver reads than Creek B, after accounting for our observation variance, is 0.839; the estimated magnitude of the difference between the two sites is 43 reads, with 95% CI of -46, 137 reads.
Variance and the Mean
A corollary here is: we can’t say anything about a difference of a few reads here or there; this is probably more noise than signal To go a bit deeper, we’d like to understand how that noise (observation variance) changes as a function of our mean number of reads μ. For example, do we have more confidence in observations with high numbers of reads than we do in observations with low numbers of reads? Should we?
In the negative binomial distribution (or at least, the version we’re using), the variance is μ+μ2ϕ such that as ϕ gets small, the variance goes to infinity… any number of observations becomes not-too-improbable, and therefore our estimated mean, μ, doesn’t have much predictive value. As ϕ gets large, the distribution becomes more tightly concentrated around the mean.
So: large ϕ means less noise.
Because it’s more intuitive to think about than the variance, let’s look at the standard deviation (SD) and the coefficient of variation (CV), which is just the standard deviation divided by the mean. The CV is useful because it immediately gives a sense of signal::noise… where the standard deviation is greater than the mean, CV >1.
As read-counts rise, what happens to the SD? It depends upon the value of ϕ.
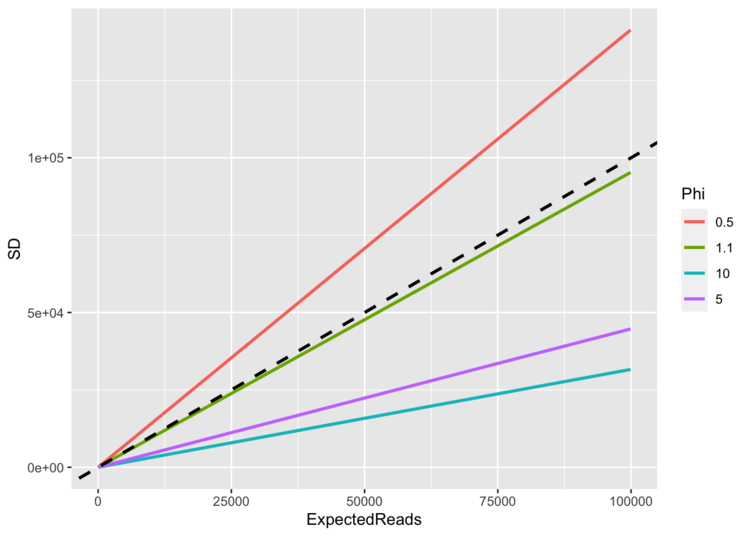
(dashed line in the plot shows 1:1 line)
When ϕ = 1, the SD ≈ the mean (until the mean gets close to zero), and so the CV is constant at 1. No matter how many reads you expect (no matter how big your mean is), the standard deviation keeps pace. When ϕ < 1, the SD > mean, and so there is a ton of scatter around our observations, and so it is more difficult to tell signal from noise. As the mean climbs, the SD climbs faster.
When ϕ > 1 and particularly as read-counts start to climb into the hundreds, the SD becomes much less than the mean, and we accordingly have higher confidence that our read-counts are telling us something. The signal is much greater than the noise. If the CV = 0.5 (ϕ=1.33), for example, a mean of 4 reads would have a SD of 2 (the 25th and 75th quantiles would be 1 and 6); a mean of 400 reads would have a SD of 200 (25th/75th = 148, 551). The chance of observing 0 reads when μ=4,ϕ=1.33 is 0.158; the chance of observing 0 reads when μ=400,ϕ=1.33 is 0.001.
And that’s why we have more confidence in the signal when we have large counts of reads… but for this intuition to be really solid, we have to know about our observation variance, captured by ϕ.
Returning to Our Example
Now that we have a better sense of what the variance term ϕ does, what would happen in our worked example of beaver DNA if we had a noisier set of observations (i.e., our ϕ were lower, like 0.5), but we had the same observed numbers of reads?

Leaving aside the obvious issue here that the observed data don’t match the fitted distributions well anymore – which is unsurprising, since we just invented a variance term for this example, with no regard to the observed data – another thing becomes clear: when variance is high enough, the means don’t matter. We would never be able to tell these sites apart with a ϕ = 0.5 and the set of observed values that we have.
And what would happen if ϕ = 30, and our observations were the same as before?

Again, our observations haven’t changed, but their variance has, so it becomes far easier to distinguish one creek’s signal from another’s… our 95% CI on the difference between observations from these distributions is now (2, 89).
The Good News, Perhaps
Of course we would like to drop a level of replication in eDNA sampling, to save time and money and sanity, as I said before. But I hope I’ve demonstrated the value of (technical) replication here… it lets us easily distinguish signal from noise, or tell us when we can’t trust our observations as well as we’d like to.
There are a couple of bits of good news, I think.
- First, it seems likely that the variance term, ϕ, is at least reasonably consistent for a given primer set and study design. So we probably don’t have to run every sample in triplicate, but running some samples in triplicate gives us a good sense of the variance across our whole dataset.
- Second, because the variance is related to the mean, deeper sequencing depths will mean that more ASVs will be more reliable signals… that is, by increasing your sampling effort, you increase your ability to distinguish signal from noise. Which we probably knew already, but it’s worth celebrating the idea that we can decide whether or not we care about rare things in our data. If we really care about those rare things, we can make them less rare (and more reliable) by sequencing more deeply.